이 포스트는 하버드의 확률론 기초 강의를 듣고 정리한 것입니다. (edwith제공) 강의 동영상 링크

1 | Probability and Counting

표본 공간 (Sample Space) : 실험에서 가능한 모든 경우의 집합

사건 (Event) : 표본 공간의 부분집합

확률의 naive한 정의

사건 A에 대한 발생 확률을 P(A)라고 할 때, P(A) = 사건 A가 발생하는 경우의 수 / 발생 가능한 모든 경우의 수

여기서 내포하고 있는 가정은 다음과 같다.

• 모든 사건이 발생할 확률은 같다.
• 유한한 표본 공간을 가지고 있다.

그렇다면 경우의 수를 어떻게 count 할 수 있을까? → 1. 곱의 법칙

곱의 법칙 (Multiplication Rule)

n_1개의 가능한 결과가 있는 첫 번째 실험, n_2개의 가능한 결과가 있는 두 번째 실험 .. n_r개의 가능한 결과가 있는 r번째 실험이 있다고 가정할 때, 이 모든 실험에서 발생 가능한 모든 경우의 수는 n_1 * n_2 * … * n_r 이다. 트리 구조로 표현해보면 쉽게 알 수 있다.

이항 계수 (Binomial Coefficient)

n명의 사람이 있을 때 k명을 선택하는 경우의 수 (여기서 순서는 관계 없다.)

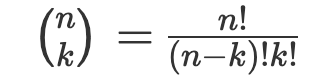
크기가 n인 집합에서 만들 수 있는 크기가 k인 부분 집합의 수를 계산할 때, 두 가지 고려할 사항이 존재한다.

1. 복원 여부 : 하나를 고른 후 그 하나를 내려놓아 다시 고려할지, 고른 하나를 다음번 시도에 포함시키지 않을지 여부
2. 순서가 상관 있는지

이 두 가지 사항을 고려한 경우의 수들은 아래와 같이 존재하게 된다.