CS231n lecture 2
Cs231n, Deeplearning, Cnn이 포스트는 stanford의 CS231n강의를 듣고 정리한 것입니다. 강의 동영상 링크 cs321n github
Lecture 2 | Image Classification
이미지 분류는 컴퓨터 비전 분야에서 가장 중요한 문제로 정의된다. 하나의 이미지가 input으로 주어지고, ouput으로 원래 정해져 있는 라벨들 중에서 가장 가까운 라벨을 골라 낸다. 이러한 이미지 분류기의 API를 작성해 본다면 아래와 같다.
def classify_image(image):
# Some magic here?
return class_label
우리의 이미지 분류 알고리즘은 위의 코드에서 # some magic here? 부분에 들어가게 될 것이다. 하지만 문제는 이렇게 이미지를 분류할 직관적인 알고리즘이 존재하지 않는다는 것에 있다.
Semantic gap
인간은 이미지를 볼 때 이 이미지에 어떤 물체가 있고 어떤 정보들을 가지고 있는지 등 이미지를 전체적으로 보지만, 컴퓨터에게 이미지는 단지 많은 양의 숫자들이 그리드 상에 있는 것에 불과하다. 따라서 하나의 물체를 다양한 각도에서 찍거나, 모양을 변형하거나, 조명 상태를 달리해 여러 장의 이미지를 생성했을 때, 인간은 이 이미지들을 원래의 물체로 분류할 수 있지만 컴퓨터는 그러지 못한다. 이러한 차이를 semantic gap 이라 부른다. 인간은 이 이미지들을 semantic하게 이해하지만 이미지 내부의 숫자들은 매우 달라지기 때문에 컴퓨터는 이해하지 못하는 차이가 발생하는 것이다.
컴퓨터 비전의 관점에서, 아래와 같은 해결해야 할 문제들이 존재한다.
- Viewpoint variation
- Scale variation
- Deformation
- Occlusion
- Illumination conditions
- Background clutter
- Intra-class variation
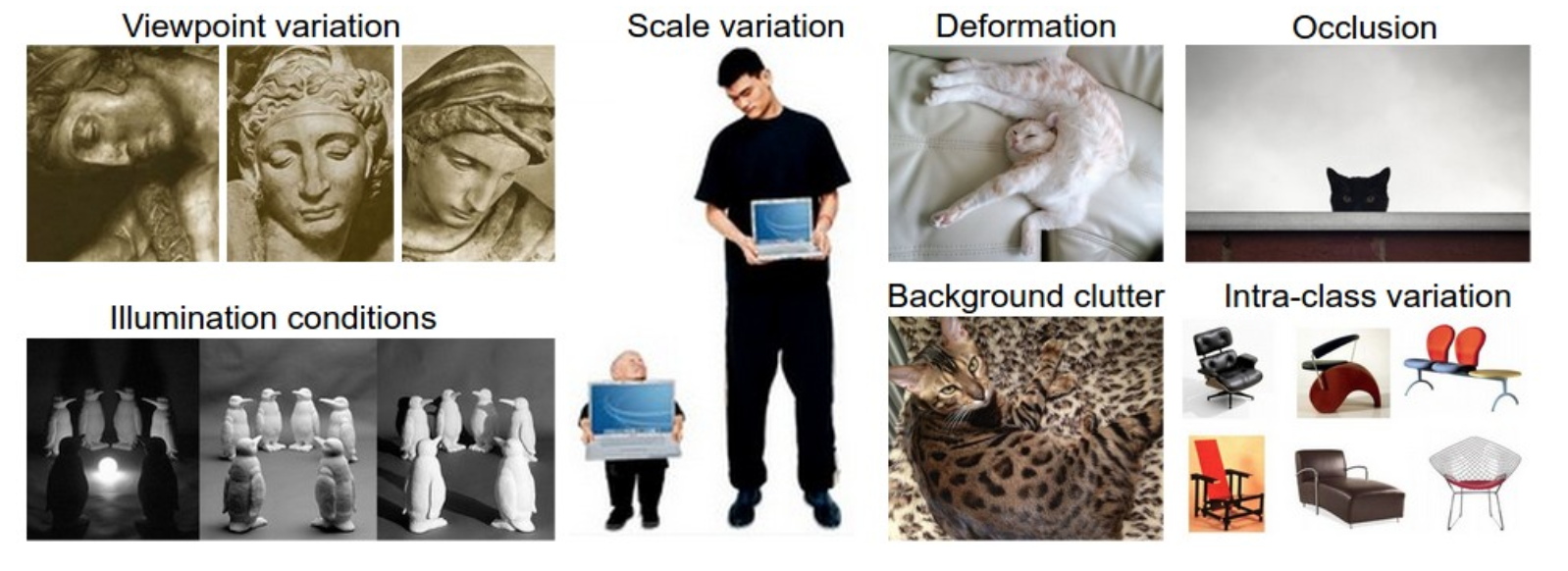
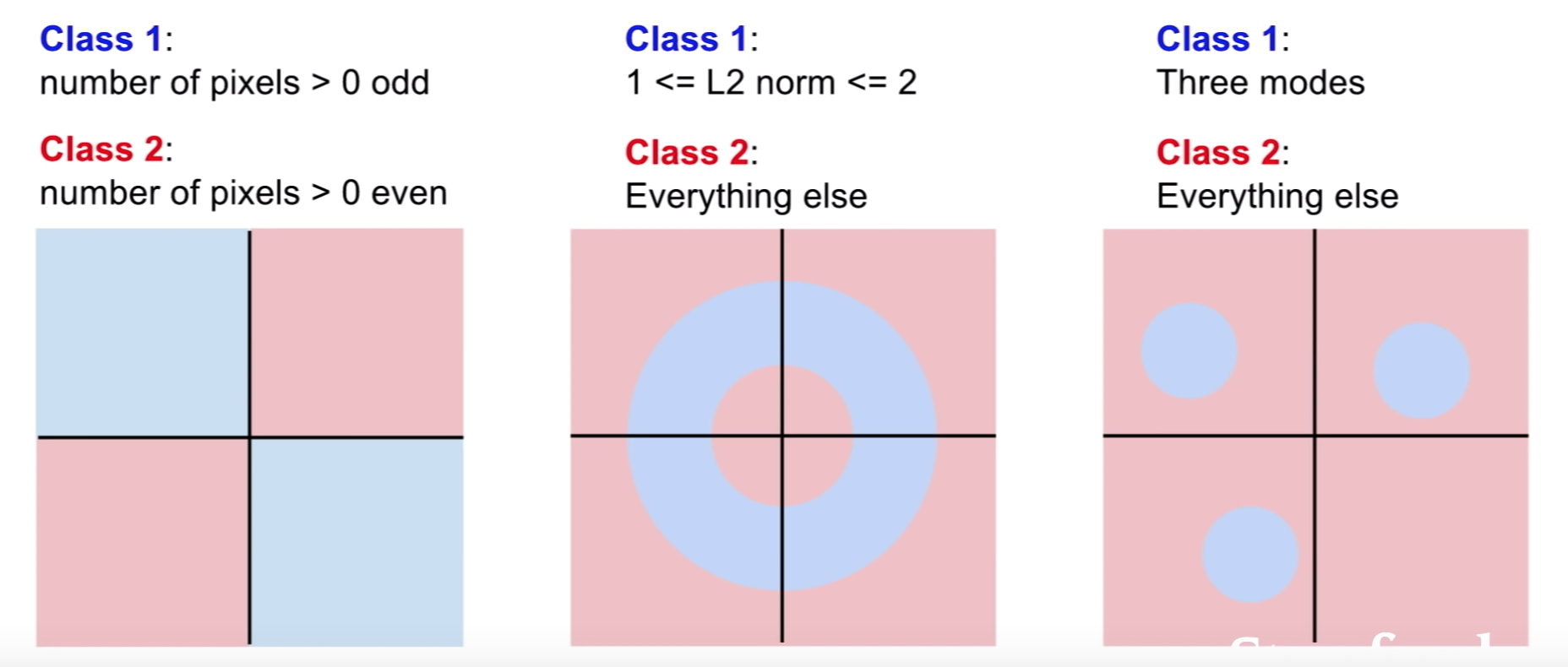
좋은 이미지 분류기는 각 클래스 간의 감도를 유지하면서 동시에 이런 다양한 문제들에 대해 변함없이 분류할 수 있는 성능을 유지해야 한다.
다시 이미지 분류기 API를 작성하는 것으로 돌아가면, 지금까지 이미지 분류를 위한 다양한 시도들이 있었다

예를 들어 이미지의 엣지를 따고 corner를 계산해서 고양이인지 판별하는 방식이 있겠다. 이 방식은 처음에 시도되었으나 당연하게도 좋은 방법이 아니다. 일단 매우 복잡하기 때문에 잘 작동되지 않고, 고양이가 아닐 경우(트럭, 개 등등)는 또 그 계산하는 것들을 새로 만들어 주어야 한다(Not scalable approach).
Data-driven approach
data-driven approach는 클래스의 특징들에 관한 알고리즘을 적어 분류하는 대신
- 인터넷에 가서 엄청나게 많은 이미지들을 모은다
- 이 이미지들을 머신러닝 분류기로 학습시킨다
- 평가하고 사용한다
즉, 코드를 통해 이미지를 직접적으로 분류하지 않고, 컴퓨터에게 각 클래스에 대해 수많은 예제를 주고 나서 이 예제들을 보고 시각적으로 학습할 수 있도록 하는 학습 알고리즘을 개발한다. 이 방법은 라벨화가 된 이미지들 training dataset이 학습을 위해 필요하다. 이 수업에서는 CIFAR 10 dataset을 사용한다.
- Input(입력): 입력은 N 개의 이미지로 구성되어 있고, K 개의 별개의 클래스로 라벨화 되어 있다. 이 데이터를 training set으로 사용한다.
- Learning(학습): 학습에서 할 일은 트레이닝 셋을 이용해 각각의 클래스를 학습하는 것이다. 이 과정을 training a classifier 혹은 learning a model 이란 용어를 사용해 표현할 수 있다.
- Evaluation(평가): 마지막으로 새로운 이미지에 대해 어떤 라벨로 분류되는지 예측해봄으로써 분류기의 성능을 평가한다. 새로운 이미지의 라벨과 분류기를 통해 예측된 라벨을 비교할 것이다. 직관적으로, 많은 예상치들이 실제 답과 일치하기를 기대하는 것이고, 이 것을 우리는 ground truth(실측 자료) 라고 한다.

이 접근법을 이용해 이미지 분류 파이프라인을 아래와 같이 공식화할 수 있다.
- Input(입력): 입력은 N 개의 이미지로 구성되어 있고, K 개의 별개의 클래스로 라벨화 되어 있다. 이 데이터를 training set으로 사용한다.
- Learning(학습): 학습에서 할 일은 트레이닝 셋을 이용해 각각의 클래스를 학습하는 것이다. 이 과정을 training a classifier 혹은 learning a model 이란 용어를 사용해 표현할 수 있다.
- Evaluation(평가): 마지막으로 새로운 이미지에 대해 어떤 라벨로 분류되는지 예측해봄으로써 분류기의 성능을 평가한다. 새로운 이미지의 라벨과 분류기를 통해 예측된 라벨을 비교할 것이다. 직관적으로, 많은 예상치들이 실제 답과 일치하기를 기대하는 것이고, 이 것을 우리는 ground truth(실측 자료) 라고 한다.
따라서 우리는 새로운 API를 정의 할 수 있다.
- 하나는 train → input: 이미지와 라벨, output: 모델
- 하나는 predict → input: 모델과 테스트 이미지, ouput: 라벨
그럼 이 방법으로 가장 간단한 분류기를 하나 만들어보자.
Nearest Neighbor
nearest neighbor(NN)는 이미지간의 거리를 계산하여 가장 이웃에 위치한 이미지를 근거로 class를 결정한다. 결국 가장 비슷한 이미지를 찾는 셈이다. 이 분류기는 CNN과 아무 상관이 없고 실제 문제를 풀 때 자주 사용되지 않지만, 이미지 분류 문제에 대한 기본적인 접근법을 알 수 있도록 한다.
NN Implementation-distance metric
이 때 이미지의 거리를 어떻게 계산할 것인가? 이웃에 위치한 이미지들이 비슷한 이미 지들이라고 할 때, 이 비슷하다 라는 것을 어떻게 정의할 수 있을까?
여기서 정의하는 가장 간단한 방법 중 하나는 이미지를 각각의 픽셀값으로 비교하고, 그 차이를 모두 더하는 것이다. 이 방법의 결과는 모든 픽셀값 차이의 합이며, L1 distance라고 부른다.
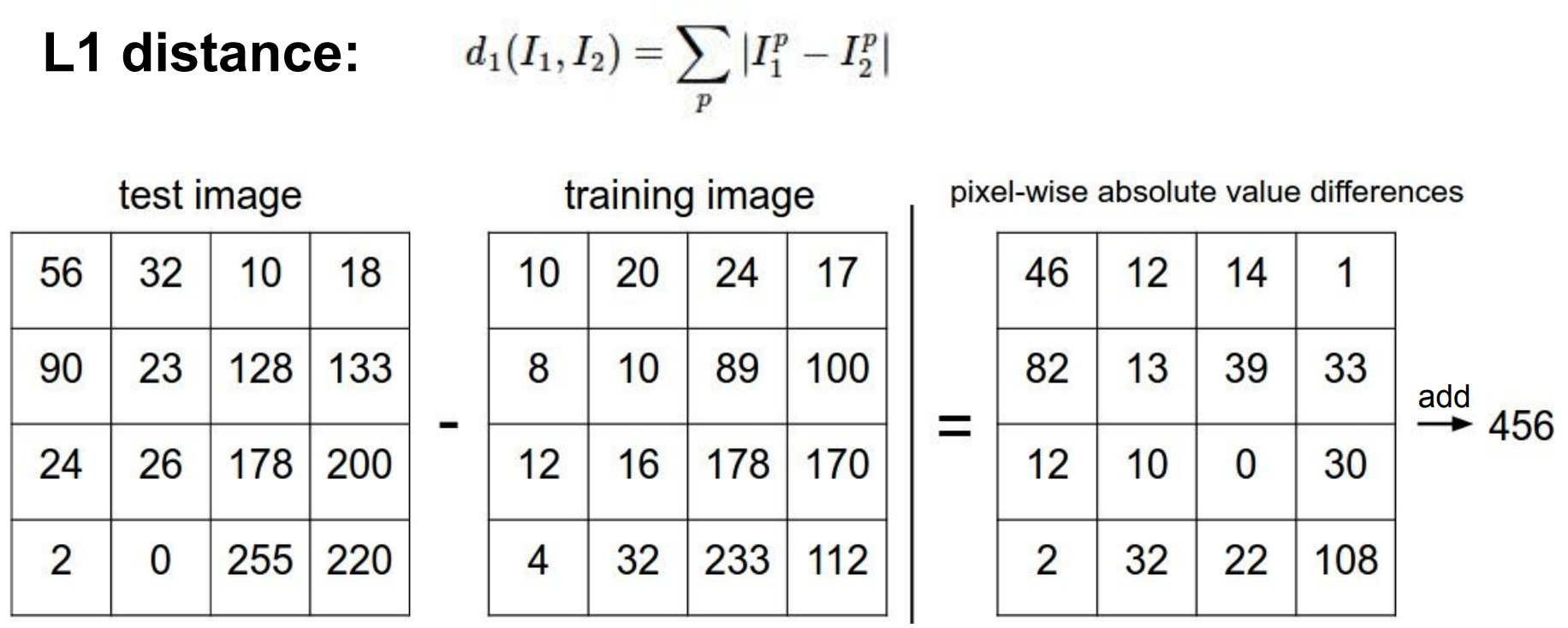
L1 distance
Implementation-dataset
사용할 데이터셋은 CIFAR-10이라는 데이터셋이다. 이 데이터셋은 32x32, 60000개의 컬러 이미지로 이루어져 있고 각각의 이미지가 10개의 클래스 중 하나의 클래스로 라벨화되어있다.
Implementation
nearest neighbor classifier를 위한 API는 다음과 같다.
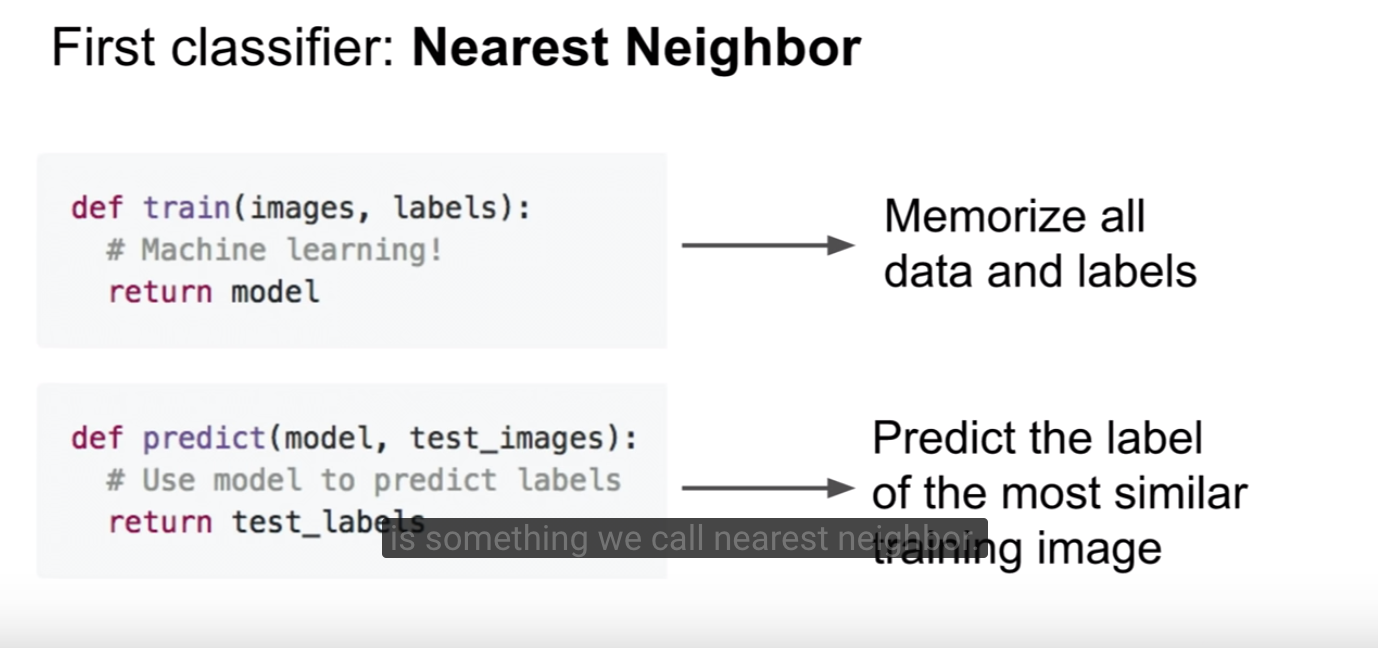
train 단계에서는 이미지들을 단순히 저장만 하고, predict단계에서 저장한 이미지들을 모두 비교하며 가장 가까운 이웃을 찾아 라벨을 예측한다. 코드로 구현하면 다음과 같다.
import numpy as np
class NearestNeighbor(object) :
def __init__(self):
pass
def train(self, X, y):
# nearest neighbor 분류기는 단순히 모든 학습 데이터를 기억해둔다.
self.x_train = X
self.y_train = y
def predict(self, X):
num_test = X.shape[0]
y_pred = np.zeros(num_test, dtype=self.y_train.dtype)
for i in range(num_test):
# i 번째 테스트 이미지와 가장 가까운 학습 이미지를
# L1 거리(절대값 차의 총합)를 이용하여 찾는다.
distances = np.sum(np.abs(self.x_train - X[i,:]), axis = 1)
min_index = np.argmin(distances) # 가장 작은 distance를 가지는 인덱스
y_pred[i] = self.y_train[min_index] # 가장 가까운 이웃의 라벨로 예측
return y_pred
# load CIFAR-10 dataset
from keras.datasets import cifar10
# x_train : all of images of training set
# y_train : labels of training set
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
xtr_rows = x_train.reshape(x_train.shape[0], 32 * 32 * 3)
xte_rows = x_test.reshape(x_test.shape[0], 32 * 32 * 3)
print(xtr_rows.shape)
print(xte_rows.shape)
# # normalize data
# x_train = x_train / 255.0
# x_test = x_test / 255.0
# # print shape
# print(x_train.shape)
# print(x_test.shape)
nn = NearestNeighbor()
nn.train(xtr_rows, y_train) # 학습 이미지/라벨을 사용하여 분류기 학습
y_test_predict = nn.predict(xte_rows) # 테스트 이미지들에 대해 라벨 예측
# 성능프린트
print('accuracy: %f' %(np.mean(y_test_predict == y_test)))
이 분류기의 성능을 평가해 보면, train : fast O(1), predict : slow O(N)이다. 이것은 별로 좋지 못하다.(반대의 경우는 ok)
Hyperparameters
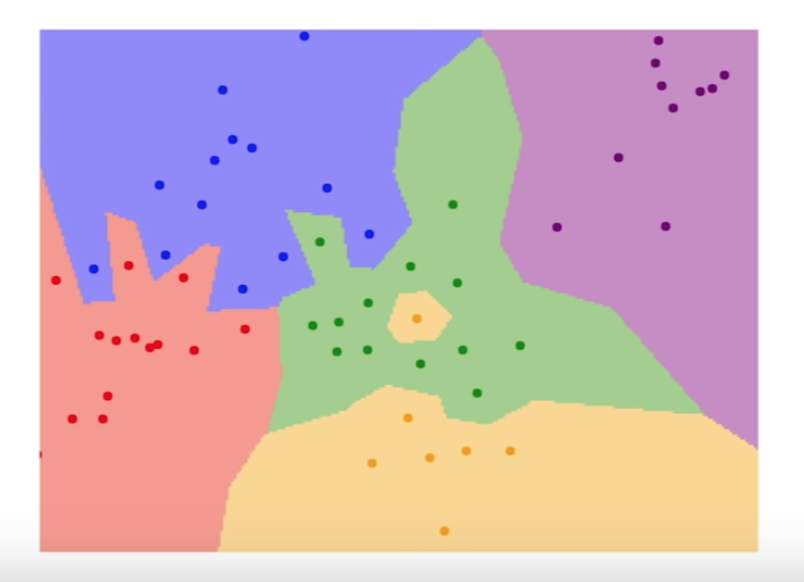
decision regions of a nearest neighbor classifier
k-Nearest Neighbor
실제로 코드를 돌려 나온 결과를 확인하면, 이미지들을 단순히 픽셀값이 비슷한지 아닌지로 비교하기 때문에 결과가 좋지 않다는 것을 알 수 있다. 만약 가장 가까운 이웃으로 라벨을 결정하지 않고 top 5의 이미지들의 라벨 중 가장 많은 라벨을 현재 이미지의 라벨로 결정한다면 더 좋은 결과를 낼 수 있을 것이다. 이것이 k-Nearest Neighbor classifier이다. 여기서 k는 몇 개의 최근접 이웃을 가지고 올것인지에 대한 파라미터로 볼 수 있다.
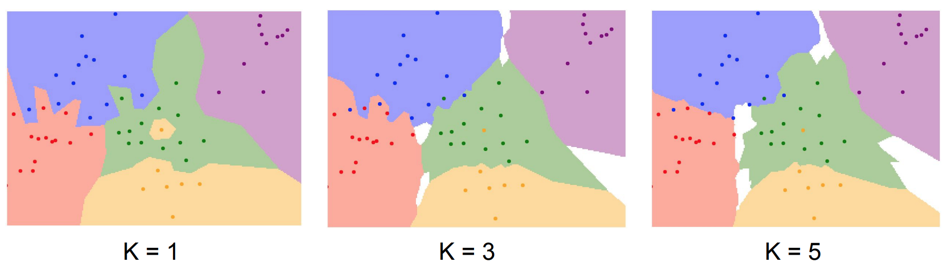
k-Nearest Neighbor 분류기를 사용하면 k값이 올라감에 따라 경계면이 흐려지고 있는 것을 확인할 수 있다.
Distance Metric
또한 다른 방법으로 이미지간의 거리를 결정할 수도 있을 것이다. 이전에 우리는 L1 distance를 사용했는데, 또다른 선택으로 유클리디안 거리를 계산하는 L2 distance를 선택할 수도 있다.
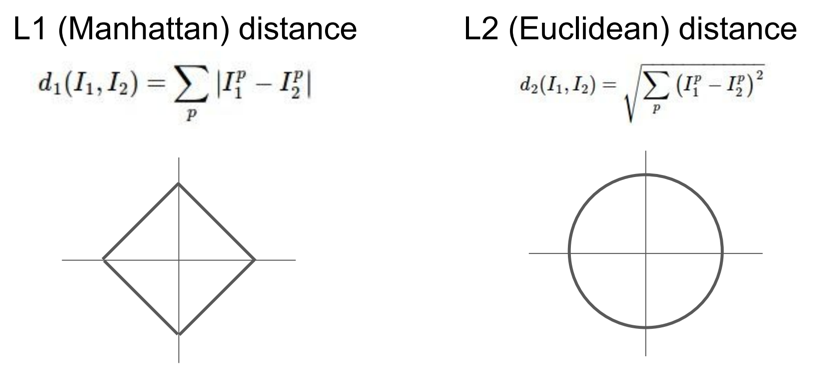
이 거리 함수들을 사용했을 때 실제 정확도는 L1 이 조금 더 높다.
L1 vs L2 : Maybe if your input features, if the individual entries in your vector have some important meaning for your task, then maybe somehow L1 might be a more natural fit. But if it’s just a generic vector in some space and you don’t know which of the different elements, or you don’t know what that actually mean then maybe L2 is slightly more natural.
L1 , L2 distance를 사용하는 게 정확도는 떨어지지만, 어떤 데이터 타입(여기서는 이미지를 이용했지만, text paragraph간의 거리를 구하는 데에도 general하게 적용할 수 있다.)이든지 적용할 수 있다는 점에서 처음 배우는 사람들이 시도할 만하다.
L2는 어느 구간에서도 미분이 되지만, L1는 미분이 되지 않는 구간이 존재한다. 과거에는 이 이유로 L2를 많이 사용했지만 L1이 성능이 조금 더 좋다는것이 밝혀져 최근은 L1을 많이 쓰기도 한다.
So, the question is what exactly does this nearest neighbor algorithm look like when you apply it in practice?
아래 그림을 보면, 두 개의 다른 distance를 사용한 decision region 간의 모양이 다르다는 것을 확인할 수 있다. L1 을 사용한 경우에는 경계의 모양이 coordinate를 따른다.(x, y 축에 대해 수직이거나 사선을 유지하고 있음)

here our training set consists of these points, color of the point represents the category
K and distance → we call they are hyperparameters : choices about the algorithm that we set rather than learn → very problem-dependent : 일단 다 실험해보고 좋은거를 고른다
L1 → coordinate dependent 각각의 벡터가 각각 의미를 가지고 있으면 L1을 쓰는 것이 좋다고 말하는듯. 걍 문제에 따라 다르다
Setting Hyperparameters
hyperparameters in k-nearest neighbors : Distance metric and K
Idea 1 choose hyperparameters that works best on the data : BAD idea
Idea 2 Split data into train and test, choose hyperparameters that works on test data
트레이닝/테스트 데이터로 나눈다. 그리고 트레이닝 데이터셋을 이용해 하이퍼파라미터를 바꿔가며 훈련하고 훈련된 분류기를 테스트 데이터셋에 적용해 가장 좋은 성능을 보이는 것을 선택한다 : BAD idea
→ 우리의 목표는 모델이 실제 세상에서 처음 보는 데이터를 입력받았을 때 어떻게 작동하는가에 있다. 따라서 test dataset은 실전에서 우리의 방법이 어떤 식으로 작동되는지 추정하는 용도로만 쓰여야 한다. (The point of the test set is to give us some estimate of how our method will do on unseen data that’s coming out from the wild.) 따라서 만약 우리가 이 방법을 써서, 다른 종류의 하이퍼 파라미터를 사용한 다른 알고리즘들을 트레이닝 시켜두고, 테스트셋에서 가장 좋은 성능인 것을 선택한다면, 우리의 방법은 테스트셋에서는 잘 작동하지만 처음 보는 데이터셋에서는 퍼포먼스를 내지 못할 것이다. 따라서 이 방법은 절대 하면 안된다
Idea 3 Split data into train, val, and test; choose hyperparameters on val and evaluate on test → much more common
데이터셋을 세 개로 나눈다. 1. train set , 2. validatoin set : hyperparameter를 정하는데 사용 3. test set : run it only once
What we typically do is go and train our algorithm with many different choices of hyperparameters on the training set, evaluate on the validation set, and now pick the set of hyperparameters which performs best on the validation set. And after all of development ,debugging, and so on, then take the best performing classifier on the validation set and run it once on the test set.
This is really important that you keep a very strict separation between the validation data and the test data
another strategy: cross validation
hyperparameter결정을 위한 다른 방법: 데이터셋이 작을 때 사용되며, 딥러닝에서는(데이터셋이 많은 경우) 잘 사용하지 않는다.
Question1. what is the difference between the training and the validation set?
(case for the k-nearest neighbor classifier) Our algorithm will memorize everything in the training set, and now we’ll take each element of the validation set and compare it to each element in the training data and then use this to determine what is the accuracy of our classifier when it’s applied on the validation set. Where your algorithm is able to see the labels of the training set, but for the validation set, your algorithm doesn’t have direct access to the labels. we only use the labels of the validation set to check how well our algorithm is doing.
실제 활용 교차 검증은 계산량이 매우 많아지기 때문에, 실제로 사람들은 교차 검증보다 하나의 검증 셋을 정해놓는 것을 선호한다. 보통은 학습 데이터의 50% ~ 90% 정도를 학습 용으로 쓰고 나머지를 검증 데이터로 활용하는데, 검증 데이터셋의 크기는 여러 가지 변수들에 의해 영향을 받는다. 예를 들어, hyperparameter 개수가 매우 많다면, 검증 데이터셋의 크기를 늘리는게 좋을 것이다. 검증 셋에 있는 데이터의 개수가 매우 적다면 (수백 개 정도), 교차 검증 방법을 사용하는 것이 더 안전하다. 보통은 3-fold, 5-fold, 10-fold 교차 검증을 주로 많이 사용한다.
Usage on Images
k-Nearest Neighbor on images never used
- test 단계가 너무 느리다. (training 단계는 빠름) → 반대가 되어야 함
- 효과적이지 않다. → 이미지들은 매우 고차원이기 때문에 L2 distance가 비슷한 이미지들을 실제로 비교해 보면 매우 다르다는 것을 알 수 있음
- 차원의 저주 → knn이 잘 동작하기 위해서는 트레이닝 데이터들이 충분히 dense해야 한다. 1차원 데이터를 충분히 커버하기 위해 4개의 점이 필요하다고 생각한다면 차원이 올라갈 수록 충분히 커버하기 위해 필요해지는 점의 개수는 exponential 하게 올라간다. 이미지는 매우 고차원의 데이터이기 때문에 이미지의 차원을 충분히 커버하는 데이터의 양은 우리가 절대 구할 수 없다. (Basically you’re never going to get enough images to densly cover this space of pixels)
Linear Classification
KNN을 이미지 분류기로 사용하는 것은 적합하지 않다. Linear Classification 또한 매우 간단한 알고리즘을 가지고 있지만, 신경망 학습과 CNN의 전체 개념을 잘 잡을 수 있게 해준다. deep neural network모델을 Lego를 쌓는 과정에 비유한다면 linear classifier는 전체 네트워크의 가장 기본적인 블록에 비유될 수 있을 것이다.
Parametric Approach
선형 분류기는 knn과 약간 다른 접근법을 가지고 있다. 앞으로 이것을 parametric model로 부를 것이다.
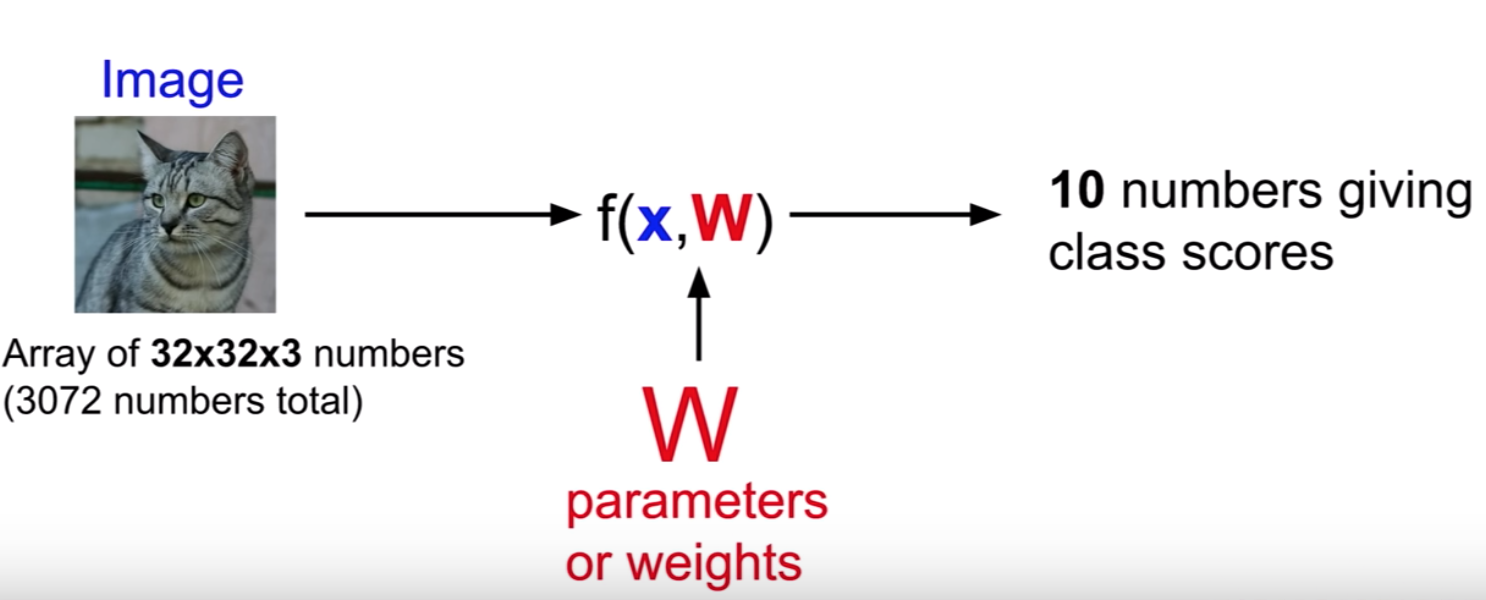
x is input data, W is parameters or wieghts
Input으로 이미지와 parameter를 받고, output으로 각 카테고리별 확률을 뱉는다. knn에서는 데이터를 보면서 test를 할 때 데이터를 사용했다면, 이 접근법에서는 우리의 training data에 대한 지식을 요약하고, 그 모든 지식들을 이 parameter에 붙인다고 할 수 있다. 이 접근법으로 우리는 test를 할 때 데이터가 필요없어지고, 오직 parameter들인 W만 필요하게 된다.
parametric approach를 요약하자면, parameter들을 모은 W와 image(클래스를 분류하고자 하는 이미지) x를 input으로 받는 함수 f가 있고, 이 함수 f는 image에 대한 클래스별 확률 내지는 가능성, 즉 score를 output으로 가진다. 그렇다면 이 함수 f는 어떤 방식으로 W와 x를 합쳐 output을 생성해낼까? 가장 간단한 방법으로는, W와 x를 곱하는 것이다. 이 방식이 바로 linear classifier이다. 여기서 그림 상의 f(x, W)는 Wx가 되고, 우리는 이 함수 f를 score function 이라고 부른다. 이 함수의 목표는 이미지의 픽셀 값들을 각 클래스에 대한 신뢰도 점수(confidence score)로 매핑시키는 것이다.
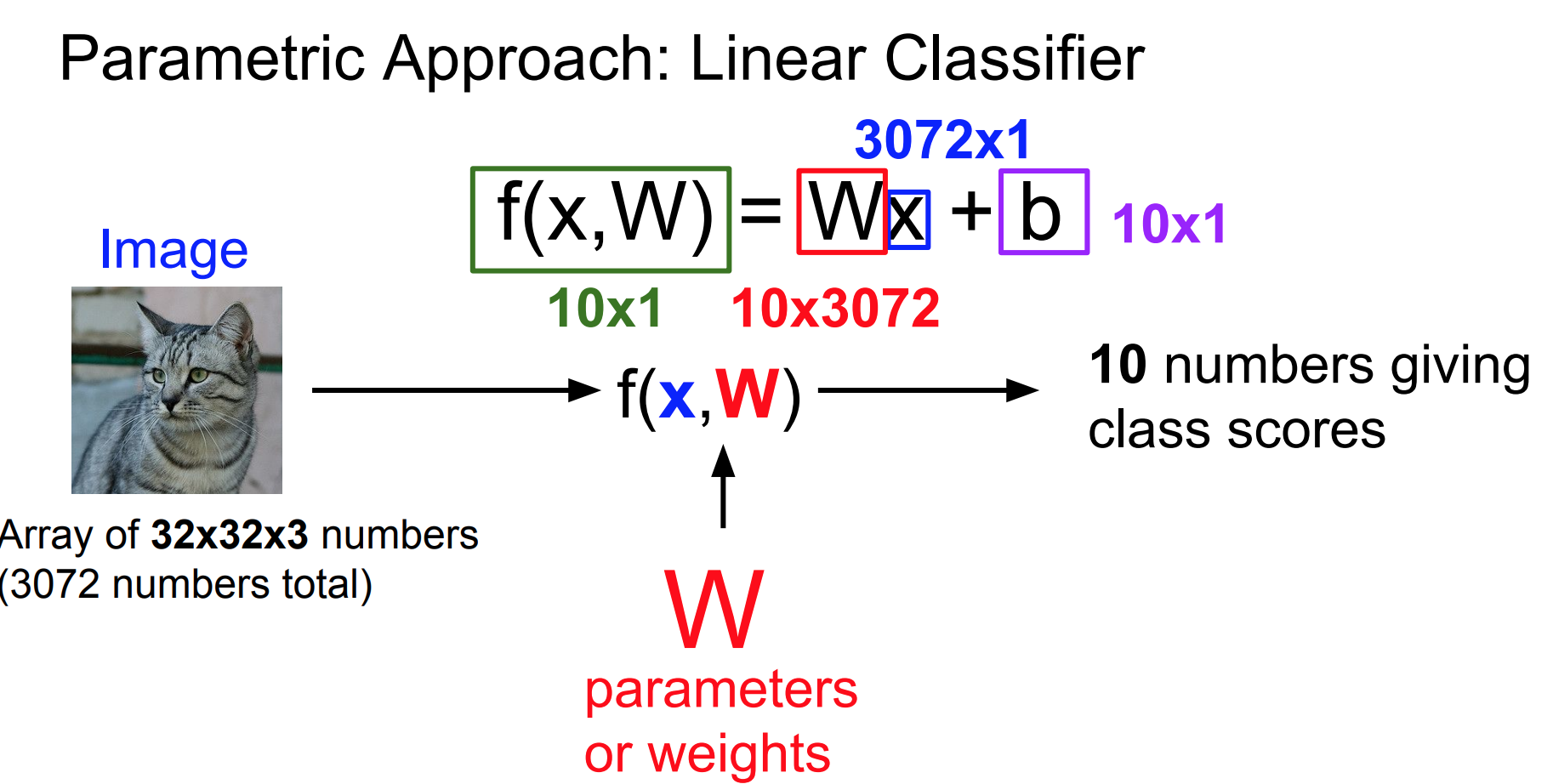
앞서 사용한 CIFAR-10 dataset을 적용해 본다.
CIFAR-10 dataset에 linear classifier를 적용해 보자. 각 이미지는 32x32x3, 즉 3072개의 픽셀로 이루어져 있고, 이것을 [3072x1] 모양을 가지는 하나의 열 벡터로 평평하게 만들어 사용한다. score function의 output은 [10x1] 모양을 가지는 벡터이고, 10은 10개의 클래스를 가리킨다. 이 벡터는 각 클래스에 대한 스코어이다. linear classifier는 W와 x를 곱해 스코어를 얻어내기 때문에, W는 [10x3072]가 된다. 슬라이드를 보면 [10x1]벡터 b를 추가로 확인할 수 있는데, b벡터는 bias벡터라고 불린다. 이 벡터는 constant vector이고, 데이터와 무관하게 클래스에 우선권을 부여한다. 예를 들어 클래스 별 데이터의 개수가 차이 난다거나 할 때 특정 클래스에 대해 우선권을 부여하는 역할을 하게 된다. 이 벡터는 실제 데이터인 x와 아무런 상호 작용을 하지 않지만, 출력 스코어 값에는 영향을 주기 때문에 bias 벡터라고 불린다. (만약 고양이 클래스의 이미지가 개 클래스의 이미지보다 더 많을 때, 고양이 클래스에 해당하는 bias element는 더 높게 설정될 것이다.)
예시: with an image with 4 pixels, and 3 classes
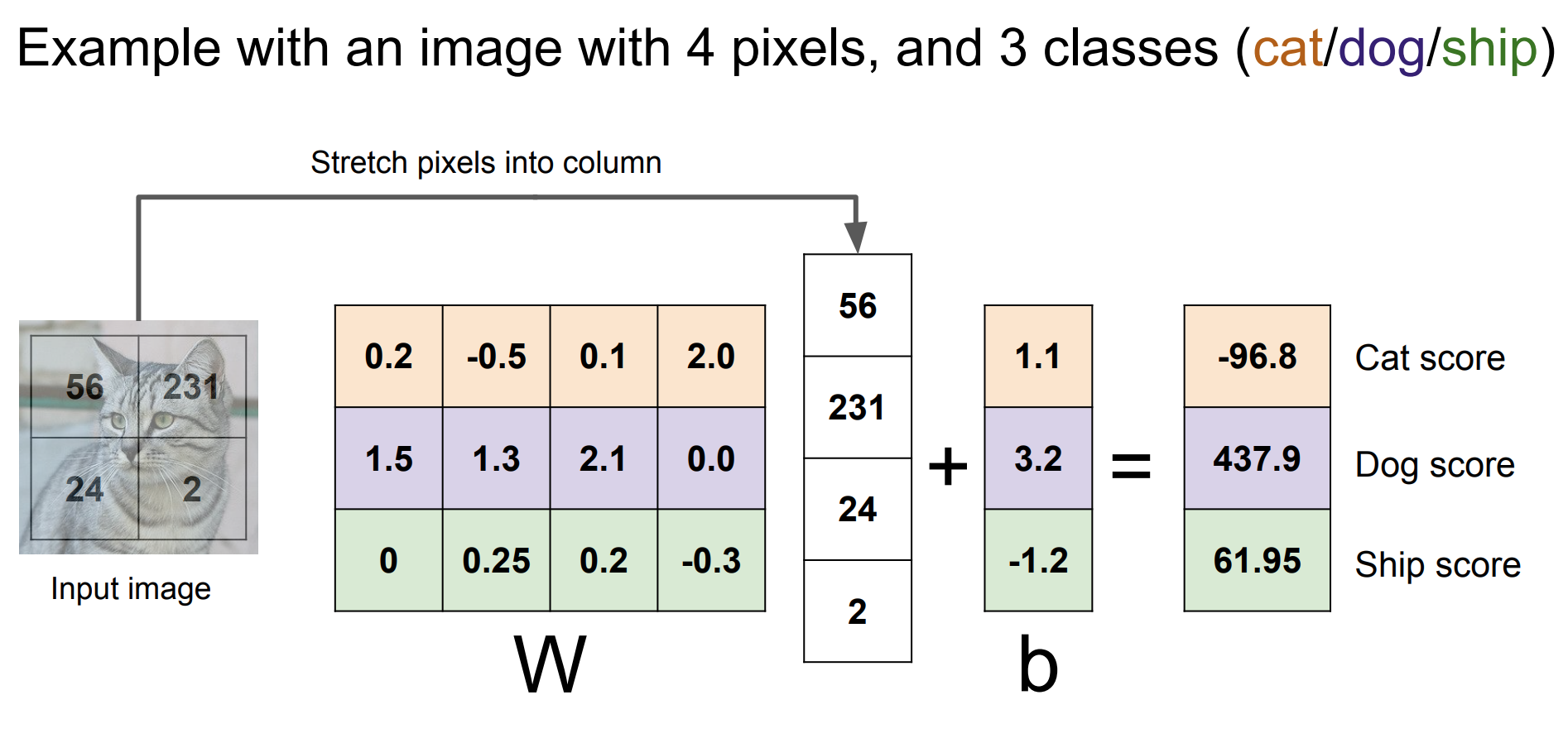
위 그림은 시각화를 위해 이미지가 2x2 픽셀로 이루어져 있다고 가정하여 도식화한 것이다. 각 색깔은 각 클래스를 의미한다고 해석할 수 있다. 주의해야 할 점은 도식의 파라미터 값은 이 이미지를 dog라고 해석하고 있다는 점이다.
선형 분류기의 다양한 분석
선형 분류기는 다양한 방식으로 분석될 수 있다. 선형 분류기의 파라미터 W가 의미하는 바에 대해 다양한 방식으로 분석해 본다.
템플릿 매칭으로서의 선형 분류기 해석
W의 각 행은 각 클래스에 대한 template으로 해석될 수 있다. template은 각 클래스에 대해 해당 클래스의 평균 이미지라고 보면 된다. 이 관점에서, 이미지의 스코어들은 템플릿들을 이미지와 내적(dot product 혹은 inner product)을 통해 비교되고, 가장 잘 맞는 템플릿이 무엇인지에 대한 스코어이다. 이 관점에서, 학습은 각 클래스의 템플릿을 배우는 과정이라고 할 수 있다. 학습을 한 후 각 클래스별로 한 장의 템플릿을 사용해 가장 잘 맞는 템플릿으로 클래스를 결정하는 셈이다. 하지만 이 방법으로는 각 클래스에 대해 한 장의 템플릿으로만 비교하게 되기 때문에 좋은 방법이라고 볼 수 없다.

CIFAR-10 dataset을 선형분류기를 통해 학습시켜 나온 각 클래스별 템플릿이다.
고차원 공간 상의 점에 대한 비유
이미지들을 고차원 열 벡터로 펼쳤기 때문에, 우리는 각 이미지를 고차원 공간 상의 하나의 점으로 생각할 수 있다. 선형 분류기는 이 공간에 직선을 그어 클래스를 구분하는 것으로 해석할 수 있다. 이를 2차원으로 시각화하면 아래와 같다.
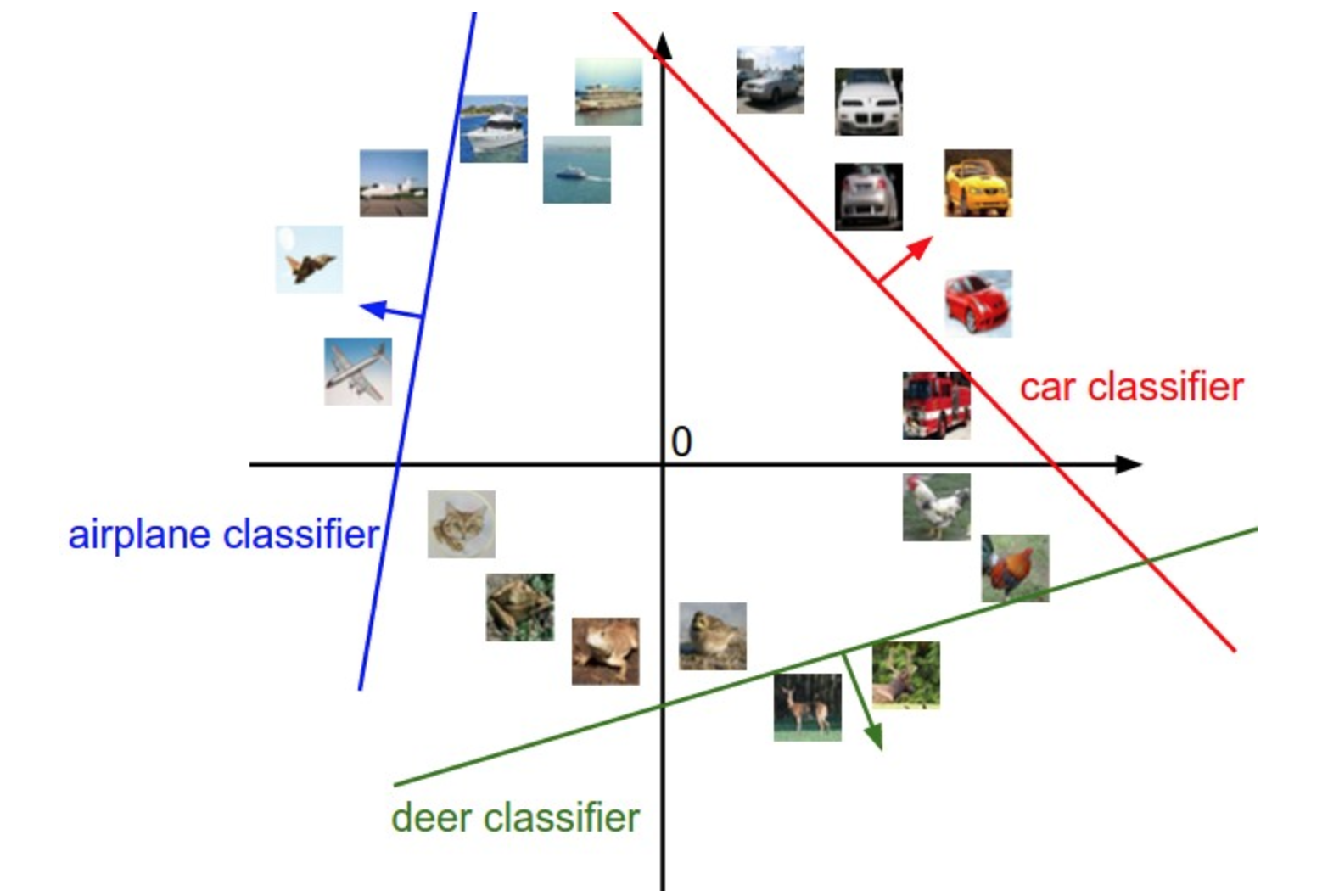
선형 분류기의 한계
선형 분류기를 공간 상에 직선을 그어 클래스를 구분하는 것이라고 해석했을 때, 아래와 같은 그림에서는 클래스를 분류할 적절한 직선을 그릴 수 없다.